| Fraktaler Exkurs | |
|
Während die jedem vertraute euklidische Geometrie lediglich die Regeln zur Konstruktion von Objekten im 1-, 2- oder 3- (also ganzzahlig-) dimensionalen Raum kennt (z. B. von Punkt, Gerade, Quadrat, Kreis, Würfel, Pyramide u. a.), liefert die fraktale Geometrie eine Sprache zur Beschreibung komplexer Formen mit gebrochenen (lat. fractum) Dimensionen, der Fraktale. Mit ihrer Hilfe lassen sich die Ordnungsprinzipien in vermeintlich chaotischen Formen und Strukturen zeigen, z. B. das Prinzip der Selbstähnlichkeit [1]: Ausschnitte einer Struktur gleichen ihr selbst: ein Ast ähnelt dem Baum, ein Zweig dem Ast, die Veräderung im Blatt dem Zweig. Eine Vielzahl natürlicher Formen hat deshalb fraktale Eigenschaften - ganz im Unterschied zu geometrisch idealisierten Gebilden wie einer Kugel, die in der Natur nicht vorkommt. Anders als die Begrenzungslinien eines Dreiecks sind die Ränder fraktaler Strukturen nicht glatt, sondern unendlich rauh - jede Vergrößerung zeigt neue Details. Natürliche Strukturen wie Wolken, Gebirge, Küsten- oder tektonische Bruchlinien, Blutgefäßsysteme, Pflanzenformen oder mineralische Oberflächen sind scheinbar unüberschaubar komplex, besitzen tatsächlich aber eine geometrische Regelmäßigkeit, die sogenannte Skaleninvarianz [2]: Unabhängig von der Auflösung/Skalierung findet man immer wieder die strukturtypische Grundform. Der wichtigste Dialekt der fraktalen Sprache ist die lineare fraktale
Geometrie. Seine 'Grammatik' enthält Vorschriften zur Herstellung
(Verkleinerung, Verdopplung) und Neuanordnung (Verbindung, Verschiebung,
Drehung, Spiegelung, Scherung usw.) von Kopien eines Ausgangsmusters.[3]
Derartige Transformationen führen unabhängig vom Ausgangsmuster zu einem
speziellen fraktalen selbstähnlichen Muster. Beispiele dafür sind die
Koch'sche Schneeflockenkurve, das Sierpinski-Dreieck, die Kurven nach
Hilbert, Peano und Cesar. |
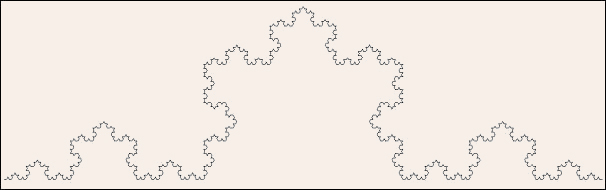 |
| Das Prinzip der Selbstähnlichkeit wird mit der Koch'schen Schneeflockenkurve, einem von drei kongruenten Teilen der Koch-Schneeflocke, besonders schön demonstriert (1904 in die Mathematik eingeführt durch den schwedischen Mathematiker Helge von Koch). Als klassischer Vertreter dieses Prinzips eignet sich der Fraktaltyp
'Iterierte Funktionensysteme' (IFS) vor allem für die Darstellung naturalistischer
Formen. Für die Modellierung fraktaler Wachstumsprozesse nutzt man den
Fraktaltyp 'L-Systeme' (Lindenmayer-Systeme) [4],
der 1968 von A. Lindenmayer als Berechnungsmethode zur Darstellung des
Wachstums lebender Organismen entwickelt wurde: |
 |
|
Beispiele für die computergenerierte Darstellung natürlicher Formen als Ergebnis fraktaler Wachstumsprozesse Es gibt unzählige Dialekte der nichtlinearen fraktalen Geometrie. Ihr prominentester Vertreter ist der quadratische Dialekt: |
|
g(z) = z² + c mit c = konstant |
| Die französischen Mathematiker Gaston Julia (1893-1978)
und Pierre Fatou (1878-1929) befassten sich um 1918 mit der Frage, was mit
einem Punkt z in der komplexen Zahlenebene [5]
geschieht, auf den man wiederholt (iterativ) die quadratische Transformation
anwendet.[6] Die Iteration rationaler Funktionen
in der komplexen Zahlenebene generiert eine Fülle von Fraktalen, die man
zu Ehren ihres Entdeckers 'Julia-Mengen' nennt. Die geometrische Anordnung
ihrer Punkte in der Ebene (z. B. auf dem Bildschirm) konnte allerdings erst
mit modernen computergrafischen Mitteln visualisiert werden. |
 |
|
Spezielle Julia-Menge als Graustufen-Bearbeitung 1980 zeigte Benoît B. Mandelbrot den mathematischen Zusammenhang zwischen den Julia-Mengen und der nach ihm benannten Mandelbrot-Menge.[7] Die klassische Mandelbrot-Menge ist die Abbildung des iterativen Prozesses nach folgendem Algorithmus: |
|
z (n + 1) = z (n)² + c mit c = variabel |
| Die grafische Darstellung der Mandelbrot-Menge wird
auch Apfelmännchen genannt. Dieses überaus komplexe und vielleicht schönste
Objekt, das die Mathematik je zugänglich und sichtbar gemacht hat, birgt
einen bizarren Reichtum an Formen und Strukturen mit immer neuen verkleinerten
Kopien des Originals. |
 |
|
Die klassische Mandelbrot-Menge besteht streng genommen nur aus der 'Küstenlinie' des Apfelmännchens. Interessant ist der Rand des Apfelmännchens, seine 'Küstenlinie'. Dort findet man filigrane Formen, die Wirbeln, Spiralen oder molekularen Gebilden gleichen. Bei stärkerer Vergrößerung zeigen sich neue, jedoch immer ähnliche Strukturen, darunter Miniaturen des Originals, in deren Randgebieten mit weiterem Zoomen neue Apfelmännchen-Generationen auftauchen - eine sich bis ins Unendliche fortsetzende Selbstähnlichkeit. Praktisch endet diese 'Reise' bei einem Zoom von ca. 1 : 20 Trillionen (immerhin das Größenverhältnis eines 19"-Monitors zum Radius des inneren Sonnensystems), weil der Mikroprozessor spätestens hier die Nachkommastellen der immer kleiner werdenden Zahlen nicht mehr berechnen kann. |
| Der praktische Anwendungsbereich nichtlinearer (fraktaler) Algorithmen zur Beschreibung komplexer dynamischer Systeme/Prozesse erstreckt sich von der Populationsgenetik (logistische Gleichung) über die Strömungsphysik (Turbulenz) bis zur Molekulartheorie der Evolution (Selektionsgleichungen). Die theoretischen Forschungen konzentrieren sich gegenwärtig verstärkt auf Fragen komplexer Muster- und Strukturbildung, d. h. sie untersuchen die Gesetzmäßigkeiten des Wechsels von Chaos und Ordnung in selbstorganisierenden Systemen von Natur und Gesellschaft. |
| |
| [1] Zur Definition
des Begriffs 'Fraktale' siehe: Mandelbrot, Benoît B.: Die fraktale Geometrie
der Natur, Basel/Boston/Berlin 1991, S.26-31. [2] A.a.O., S.30. Mandelbrot nennt Fraktale, die invariant gegenüber Maßstabstransformationen sind, skaleninvariant. - Vgl. auch Peitgen, Hans Otto/Jürgens, Hartmut/Saupe, Dietmar: Fraktale - eine neue Sprache für komplexe Strukturen in: Chaos und Fraktale, Heidelberg 1989, S.106. [3] Peitgen/Jürgens/Saupe, 1989, a.a.O. (Anm.2), S.108-111. [4] Nähere Erläuterungen dazu in: Peitgen/Jürgens/Saupe: Chaos - Bausteine der Ordnung, Stuttgart/Berlin u.a. 1994, S.503-515. [5] Die komplexen Zahlen, die Carl F. Gauß (1777-1855) einführte, gehören heute zu den elementaren, unerlässlichen Hilfsmitteln in der Naturwissenschaft. [6] Vgl. Peitgen/Jürgens/Saupe, 1989, a.a.O. (Anm.2), S.113-114. [7] A.a.O., S.114. Ausführliches zum Zusammenhang zwischen Julia-Mengen und Mandelbrot-Menge in: Peitgen/Jürgens/Saupe, 1994, a.a.O. (Anm.4), S.431-502, beschrieben. |